Heute geht es mal um ein Problem aus dem Alltag, bei dem uns Mathematik behilflich sein kann. Ich möchte mir einen Fernseher hinter meinem Schreibtisch hängen, damit ich von meinem Sessel aus Filme schauen kann. Allerdings habe ich auf meinem Schreibtisch noch eine Lampe und einen PC-Bildschirm stehen. Darüber möchte ihn nicht hängen, weil ich dann meinen Kopf unangenehm verdrehen muss. Er muss also zwischen PC-Bildschirm und Lampe positioniert werden. Zwischen diesen beiden Objekten ist ein Abstand von ungefähr 95 cm.

Ich benötige also einen Fernseher, der ungefähr 95 cm breit ist, damit er möglichst groß ist ohne dass dabei seine Bildfläche verdeckt wird. Da Fernseher allerdings nicht mir ihrer Breite, sondern ihrer Bildschirmdiagonale vermarktet werden, müssen wir irgendwie anhand der Breite Rückschlüsse auf die Bildschirmdiagonale ziehen.
Lösung mit trigonometrischen Berechnungen
Zu Hilfe kommen uns dabei die trigonometrischen Rechengesetze, aber der Reihe nach. Zuerst halten wir einmal alle Informationen fest, die wir haben. Unseren Fernseher können wir uns vereinfacht gesagt als ein Rechteck vorstellen. Gängige Fernseher haben heutzutage das Seitenverhältnis 16:9, d.h. auf 16 cm in der Breite kommen 9 cm in der Höhe dazu. Die Länge der Seite a entspricht dabei der Breite unseres Fernsehers, also gilt a=95 cm. Da wir das Seitenverhältnis kennen, können wir durch eine einfache Dreisatzrechnung auf die Höhe unseres Fernsehers schließen, was der Länge von Seite b entspricht. Es gilt also:
\(b=\text{95 cm}*\frac{1}{16}*9=\text{53,4375 cm}\)Nun stellt sich jetzt nur noch die Frage was die Länge unserer Bildschirmdiagonale c ist. Wenn wir diese nun zusammen mit den anderen Daten in eine Grafik einzeichnen sehen wir, dass wir ein rechtwinkliges Dreieck haben und c unsere Hypotenuse ist.
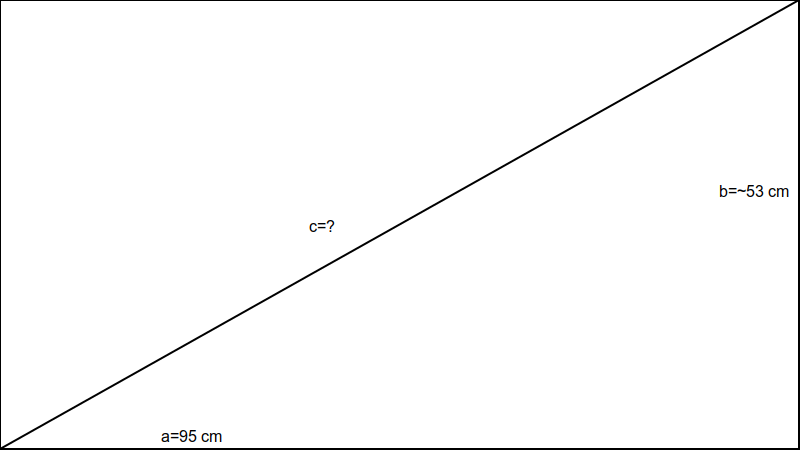
Das bedeutet, dass wir die Bildschirmdiagonale ganz einfach mit dem Satz des Pythagoras ausrechnen können. Es gilt also:
\(c=\sqrt{a^2+b^2}=\sqrt{(95 cm)^2 + (53,4375 cm)^2} = ~109 cm\)Als allgemeine Formel für eine beliebige Bildschirmbreite a können wir außerdem festhalten:
\(c=\sqrt{a^2+(\frac{9a}{16})^2}\)Die Bildschirmdiagonale beträgt also ungefähr 109 cm, was bedeutet, dass ein 42″-43″ Fernseher genau das Richtige für mich ist.
Wenn du auf der Suche nach einer musikalischen Erklärung für den Satz des Pythagoras bist, kann ich dir dieses Video empfehlen: